Artificial Intelligence and Collective Intelligence (AI/CI)
The next breakthrough in AI could be hidden in the dance of birds flocking in the sky.
Neural Networks and their associated field of Deep Learning are ubiquitous in today’s tech sector. Due to dazzling breakthroughs in recent years, such as beating the world’s best Go player, solving the decades-long protein folding problem, and of course the introduction of state-of-the-art large language models (LLMs), Artificial Intelligence (AI) has become a commodity term in society at large. Progress appears to be dizzying, with the world’s largest tech companies pumping vast amounts of resources into the sector. Therefore, we ask ourselves: what does the future hold? Are the architectures powering today’s LLMs sufficient to build truly intelligent machines, or will we remain stuck in a mix of encyclopedic knowledge and pre-school reasoning?
In order to answer this question, it is worth probing these architectures to determine potential pitfalls and limitations. For example, despite impressive results, machine learning models are still highly dependent on the data they are trained on, relying on large numbers of previously observed examples. The training process and subsequent model’s capabilities will be accordingly limited. This results in a lack of flexibility for new problem settings. For example, Google’s recently released experimental AI search feature offered bizarre answers to certain queries, such as recommending eating a small rock a day for a healthy diet, or adding glue to pizza (Thankfully, it did insist on non-toxic glue). Such queries were unlikely to be searched and therefore didn’t occur in the training datasets 1. Another example of incompetence in new settings: AI agents would fail at playing a video game they previously excelled at, simply because a few barely detectable pixels were modified between training and test data 2. It is questionable whether a system that isn’t able to change its behaviour in response to changing conditions can truly be called intelligent.
Therefore, the study of adaptive systems, both natural and artificial, could lead the way forward. A field of science that concerns itself with the study of adaptive systems is known as complexity theory. More specifically, it aims to understand the behaviours of systems made up of many interacting components. Such phenomena comprise self-organisation, emergence and adaptive behaviours, which can be summarised as collective intelligence. Rather than giving formal definitions, we will simply look to examples in the natural world. Starting off, we have the remarkable intelligence demonstrated by ant colonies.
Left: Trajan’s Bridge at Alcantara, built in 106 AD by Romans 3. Right: Army ants forming a bridge 4.
Through the coordination of a large number of individuals, ants are able to perform a variety of tasks. Showcasing that “Ants Together Strong”, army ants construct bridges for terrain traversal. Or rather, they become the bridges themselves. When compared to the stone (or steel) bridges built by humans, ant bridges exhibit remarkable flexibility. The width and length of the bridge can be adapted to the gap that needs to be traversed. Human bridges, on the other hand, are built for one specific location only. If it were to be taken out of its context and placed elsewhere, the bridge could no longer fulfill its intended purpose. Current deep learning architectures resemble stone bridges in this regard, rather than ant bridges. Once trained, the learned parameters of the neural network remain statically fixed. This rigidity leads to a lack of robustness, leading to failure in the face of changing conditions. This is why they fail when just a few pixels, undetectable to the human eye, are changed in their favourite videogame. Furthermore, a neural network has a very strict expectation of input structure. If it is trained on a certain number of inputs, pixels in an image for example, it cannot take a different number of pixels as input without first being re-trained. A bridge formed by ants, on the other hand, has much less rigid assumptions about the environment it perceives and acts within.
To overcome this rigidity is to bridge the gap between artificial intelligence and collective intelligence. Here again, the field of complexity science offers adequate tools. We will call this intersection of disciplines AI/CI (Not to be confused with the famous Australian rock band).
Background: Simulated Collective Intelligence
Rather than employing real-world biological systems, such as ant colonies, we make use of simulated systems within virtual environments. Complex phenomena exhibited by collections of biological agents can oftentimes be captured by relatively simple rule-sets in a simulated setting. For example, some bird species coordinate their flight across hundreds of individuals, creating mesmerising twists and turns in the air. Starlings are especially known for their collective dance, their shared undulating motion known as a murmuration.
This has been simulated using boids 5. Three simple rules govern the behaviour of each virtual bird, or boid:
Separation: Avoid collision with other flockmates
Alignment: Steer towards the average direction of local flockmates
Cohesion: Steer towards the average position of local flockmates
This is sufficient for the system to exhibit the emergence of flocking behaviour, where large numbers of individuals are coordinated in 2-dimensional or 3-dimensional space.
Left: Photograph of a starling murmuration 6. Right: 3D boids simulation 7.
Cellular Automata
While this is an intuitive introduction to simulated collective intelligence, there is another example that is even simpler, yet it allows the creation of fascinating patterns. Imagine a field of squares, like the checkerboard of a chess game. Think of a chess board where the colours are not ordered, but any square could be black or white. At the same time, the squares can change colour. Just like the behaviour of individual birds in our previous example, the colour of each square is controlled by simple rules. More specifically, the rules tell the squares whether they should flip from black to white, or vice versa, based on the surroundings of each square. I hear you say “Wait a minute, I thought this was supposed to be simple!” Okay, here’s an example. The rule book says:
If a white square has less than 2 white neighboring squares, it will turn black.
If it has 2 or 3 neighbours that are white, it will stay white.
If a white square has more than 3 neighbours, it will turn black.
If exactly 3 white squares surround a black one, the black one will turn white.
This little example is known as Conway’s Game of Life 8, which is a special case of a cellular automaton.
Conway’s Game of Life, a famous cellular automaton 9.
Also simply known as Life, its name is inspired by the fact that the squares, or cells, can live, reproduce and die. Therefore, white and black represents life and death. The rules that govern how a cell responds to its neighborhood, such as the ones outlined above, are called update rules. Given these rules, we can begin with any pattern of cells. From this starting point, the grid (fancy name for chessboard) will start changing the values of its cells, some coming alive and some dying. This changes the starting pattern, so that each cell is once again in a new neighborhood, and so on for as long as the simulation runs. At each time step, the local neighbourhood determines the alive/dead patterns of the grid, evolving the system over time. This is an example of emergent behaviour arising from the local interactions of cells, determined by the update rules. Such emergent behaviour includes the formation of large patterns that persist in time, known in the community as “spaceships” or “demonoids”, among many others. Enthusiasts are actively exploring all the possible “life forms” existing in this virtual microcosm.
Here is an interactive example of a spaceship.
Cellular automata are key in helping researchers understand the complexity of the real world. Take the example of ants forming a bridge. Each ant on its own cannot see the full picture of the bridge, it is only aware of what its neighboring ants are doing. In this sense, its neighborhood controls how the ant will behave. Collectively, a functional structure emerges, much like the spaceships of Conway’s Game of Life.
Background: Artificial Neural Networks
The origins of deep learning trace back to the first half of the 20th century, when neuroscientist Warren McCulloch and mathematician Walter Pitts thought up a simplified model of the human neuron: The McCulloch-Pitts neuron 10. This architecture was first implemented in 1958 by Frank Rosenblatt, an American Psychologist. It appears fitting that artificial neural networks, the second component of our AI/CI dichotomy, were also inspired by a complex biological system from the very beginning: the brain.
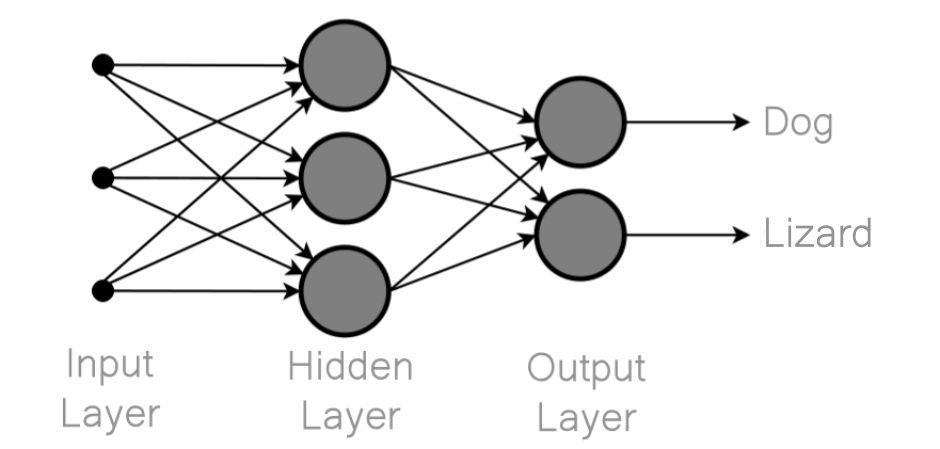
Rosenblatt’s Mark I Perceptron was initially designed to function as a “photo-interpreter”, foreshadowing the image recognition capabilities of modern neural networks. However, it was not until the 2010s that neural networks, inspired by such early architectures as the Perceptron, truly entered the mainstream following significant enhancements in complexity and performance. These models process inputs through a series of neural activation patterns, culminating in an output specific to the task—for example, identifying a dog in an image and labeling it accordingly. The learned weights in a neural network encapsulate the 'concept' of an image, which is understood through low-level features such as lines, edges, textures, and colors.
Schematic showing the structure of an artificial neural network 11.
What makes artificial neural networks so successful is that they are not manually programmed: these weights are learned through a process called training. During training, a neural network is fed a large dataset of examples (e.g., images labeled as "dog" or "not dog"). The network adjusts its internal weights iteratively to minimise the error between its predicted output and the actual label. This adjustment process, often involving techniques like backpropagation, enables the network to gradually refine its understanding of the patterns and features that distinguish a "dog" from other things, such as cats or lizards.
In certain advanced generative models like Generative Adversarial Networks (GANs) 12, once a network has been trained on such concepts, it is possible to use the model to generate images from labels, effectively synthesising new visuals based on learned data. This generative component has a symbolic connection to our following example, where we explore biological re-generation, bringing together collective intelligence and artificial intelligence.
AI/CI: Neural Cellular Automata
Now that we have introduced both the AI and the CI, it is time to combine them in a meaningful way. Let’s consider a scenario where artificial intelligence converges with biological growth and regeneration, introduced by Mordvintsev et al 13. We revisit the realm of images. It isn’t too much of a stretch to imagine a digital picture as a grid of cells, formed by the individual pixels of the image. This should ring a bell, reminding us of cellular automata, also acting on grids. Recall the alive/dead state switches flickering across the grid through time. Now, instead of simple alive/dead values for the cells, each pixel is composed of three primary colour channels: red, green and blue. For a given pixel, each of the three channels holds a real-valued number (A digital image is simply a grid of many pixels, each of which has differing values for the three primary colours).
As an example, a low-resolution drawing of a lizard on a white background has a distinct shape and colour and can be captured with relatively few pixels. This is no ordinary picture of a lizard, however. It is a sort of digital life-form, since its pixels, or cells, belong to a special kind of cellular automaton. Beyond the three colour channels, there is a fourth channel controlling the the life and death of the pixel. This alpha channel, also real-valued, indicates cell death if it reaches 0. Finally, to show that there is more to the lizard than meets the eye, there are 12 hidden channels describing each pixel. Their values aren’t seen in the image, but hold important information telling the cell how to react to its environment. These hidden channels can be seen as biological information, such as chemical or electrical signals.
This means that if something happens to a part of the lizard, changing the values of some pixels on one of its body parts, the neighboring pixels will also react to this change. For example, introducing a “wound” to the lizard by destroying several pixels will lead to a regeneration of the damaged area, based on correctly set update rules and the local neighborhood. The twist is that in this case, the update rules are learned by a neural network to achieve the desired image. This regenerative behaviour based on collective, localised information is a prime example of the adaptive behaviour of collective systems. It demonstrates how ideas from both complexity science and deep learning can be symbiotic, allowing for novel models with unprecedented capabilities.
An interactive demo of the neural cellular automaton exhibiting regeneration can be tried here.
Left to right: Image of a lizard regenerating as a neural cellular automaton 13.
Conclusions
This article was just a taste for what kind of research is being done in both disciplines, as well as their symbiotic nature. We merely touched upon the profound implications of merging collective intelligence with traditional deep learning frameworks. The rigid, static nature of current deep learning architectures, much like the unyielding Roman bridges, limits their application in dynamic, real-world environments. By integrating principles of self-organisation and adaptability observed in natural systems—exemplified by army ant bridges and starling murmurations—we move towards more versatile and resilient AI systems. This includes models that can self-regulate, self-repair, and autonomously improve over time through interactions with their environment. In doing so, artificial systems may start to closely resemble the complexity and adaptability of natural systems, of biological life itself. There is a lot to learn from systems of collective intelligence, so let’s add it to our machine curriculum.
This post was inspired by Collective Intelligence for Deep Learning, by David Ha and Yujin Tang 14. The paper is highly recommended for a deeper read with many more great examples.
References
1. "Data Void", "Information Gap": Google Explains AI Search's Odd Results. NDTV. Accessed at https://www.ndtv.com/world-news/data-void-information-gap-google-explains-ai-overviews-odd-results-5787757 (2024).
2. Qu, X., Sun, Z., Ong, Y.-S., Gupta, A. & Wei, P. Minimalistic Attacks: How Little it Takes to Fool a Deep Reinforcement Learning Policy. IEEE Transactions on Cognitive and Developmental Systems (2020).
3. Alcántara Bridge. Wikipedia (2022). Licensed under a GNU Free Documentation License.
4. Jenal, M. What ants can teach us about the market. https://www.jenal.org/what-ants-can-teach-us-about-the-market/ (2012). Licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
5. Reynolds, C. W. Flocks, Herds, and Schools: A Distributed Behavioral Model Computer Graphics (1987).
6. Baxter, W. A murmuration of starlings at Rigg. Wikimedia Commons (2013). Licensed under a Creative Commons Attribution-Share Alike 2.0 license.
7. Scheytt, P. Projeckt Sammlung (2011). Accessed at http://pl-s.de/?cat=4 with explicit permission from author.
8. Gardner, M. Mathematical Games - The fantastic combinations of John Conway’s new solitaire game ‘life’. Scientific American (1970).
9. Twidale, S. Conway’s Game of Life by Sam Twidale - Experiments with Google. https://experiments.withgoogle.com/conway-game-of-life (2016). GIF used with explicit permission from author.
10. Mcculloch, W. S. & Pitts, W. A LOGICAL CALCULUS OF THE IDEAS IMMANENT IN NERVOUS ACTIVITY Bulletin of Mathematical Biology (1943).
11. Offnfopt. Multi-Layer Neural Network-Vector-Blank. Wikimedia Commons (2015). Licensed under a Creative Commons Attribution-Share Alike 3.0 license.
12. Goodfellow, I. et al. Generative Adversarial Nets. Advances in Neural Information Processing Systems (2014).
13. Mordvintsev, A., Randazzo, E., Niklasson, E. & Levin, M. Growing Neural Cellular Automata. Distill 5, e23 (2020). Interactive article available at https://distill.pub/2020/growing-ca/. Licensed under Creative Commons Attribution CC BY 4.0 license.
14. Ha, D. & Tang, Y. Collective intelligence for Deep Learning: A Survey of Recent Developments. Collective Intelligence 1, 26339137221114874 (2022).








Such a good read!
Great read!